UAS FSA DAN GRAMMAR
Grammar (Tata Bahasa)
Tata
bahasa (grammar) bisa didefinisikan secara formal sebagai kumpulan dari
himpunan-himpunan
variabel, simbol-simbol terminal, simbol awal, yang dibatasi oleh
aturan-aturan
produksi
Suatu
tata bahasa (grammar) didefinisikan dengan 4 Tupel yaitu : V, T, P, dan S
Di
mana,
V
= Himpunan simbol variabel / non terminal
T
= Himpunan simbol terminal
P
= Kumpulan aturan produksi
S
= Simbol awal
Diagram Grammar
Penulisan Formal
Secara formal tata bahasa yang
diperoleh dari otomata adalah sebagai berikut.
V = {S, A, B, C, D,E}
T = {a, b}
P = { S → bA, S→ aB, B→ aE, B→ bC, B→ a, E→ a, E→ bB, E→ bC, E→ aE, E→ S, A→ B, A→ bA, A→ a }
S = S
Uji Input
Berdasarkan hasil dari langkah di atas maka akan didapat
hasil sebagai berikut :
INPUT : abba : ACCEPT
INPUT : aaba : ACCEPT
INPUT : bbab : REJECT
INPUT : aabb : REJECT
FSA
(Finite State Automata)
Finite state automata adalah
mesin abstrak berupa sistem model matematika dengan masukan dan keluaran
diskrit yang dapat mengenali bahasa paling sederhana (bahasa reguler) dan dapat
diimplementasikan secara nyata.
Finite State Automata (FSA)
adalah model matematika yang dapat menerima input dan mengeluarkan output yang
memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke
state lainnya berdasarkan input dan fungsi transisi. Finite state automata
tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.
Finite
State Automata dinyatakan oleh pasangan 5 tuple, yaitu:
M=(Q , Σ , δ , S , F )
Q = himpunan state
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q
M=(Q , Σ , δ , S , F )
Q = himpunan state
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q
Diagram
Penulisan
Formal
M = (Q, ∑, δ, S, F),
• Q =
{q0,q1, q2, q3, q4, q5}
• ∑ =
{0,1}
• S = q0
• F = {q3}
• δ =
|
Q
|
0
|
1
|
|
q0
|
q1
|
q2
|
|
q1
|
q5
|
q1
|
|
q2
|
q3
|
q2
|
|
q3
|
q5
|
q2
|
|
q4
|
q5
|
|
|
q5
|
q4
|
q1,q3
|
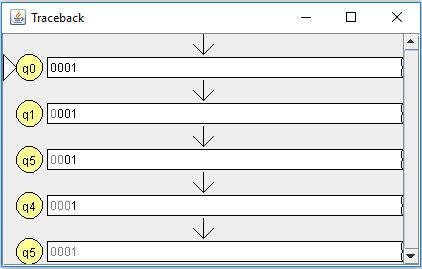
Uji
Input
Berdasarkan hasil dari langkah di atas maka akan didapat
hasil sebagai berikut :
INPUT : 1010 : ACCEPT
INPUT : 0011 : REJECT
INPUT : 1110 : ACCEPT
INPUT : 0001 : REJECT
TERIMA KASIH













Komentar
Posting Komentar